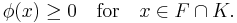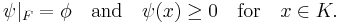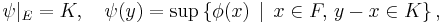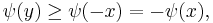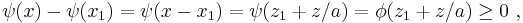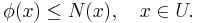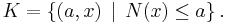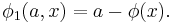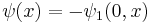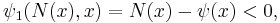M. Riesz extension theorem

The M. Riesz extension theorem is a theorem in mathematics, proved by Marcel Riesz ^[1] during his study of the problem of moments.^[2]

1 Formulation
2 Proof
3 Corollary: Krein's extension theorem
4 Connection to the Hahn–Banach theorem
5 Notes
6 References

Formulation

Let E be a real vector space, F ⊂ E a vector subspace, and let K ⊂ E be a convex cone.

A linear functional φ: F → R is called K-positive, if

$\phi(x) \geq 0 \quad \text{for} \quad x \in F \cap K.$

A linear functional ψ: E → R is called a K-positive extension of φ if

$\psi|_F = \phi \quad \text{and} \quad \psi(x) \geq 0\quad \text{for} \quad x \in K.$

In general, a K-positive linear functional on F can not be extended to a $K$ -positive linear functional on E. Already in two dimensions one obtains a counterexample taking K to be the upper halfplane with the open negative x-axis removed. If F is the real axis, then the positive functional φ(x, 0) = x can not be extended to a positive functional on the plane.

However, the extension exists under the additional assumption that for every y ∈ E there exists x∈F such that y − x ∈K; in other words, if E = K + F.

Proof

By transfinite induction it is sufficient to consider the case dim E/F = 1.

Choose y ∈ E\F. Set

$\psi|_E = K, \quad \psi(y) = \sup \left\{ \phi(x) \, \mid \, x \in F, \, y - x \in K \right\},$

and extend ψ to E by linearity. Let us show that ψ is K-positive.

Every point z in K is a positive linear multiple of either x + y or x − y for some x ∈ F. In the first case, z = a(y + x), therefore y = z/a − x. Hence

$\psi(y) \geq \psi(-x) = - \psi(x),$

therefore ψ(z) ≥ 0. In the second case, z = a(x − y), therefore y = x − z/a. Let x₁ ∈ F be such that z₁ = y − x₁ ∈ K and ψ(x₁) ≥ ψ(y) − ε. Then

$\psi(x) - \psi(x_1) = \psi(x-x_1) = \psi(z_1 %2B z/a) = \phi(z_1 %2B z/a) \geq 0~,$

therefore ψ(z) ≥ −a ε. Since this is true for arbitrary ε > 0, we obtain ψ(z) ≥ 0.

Corollary: Krein's extension theorem

Let E be a real linear space, and let K ⊂ E be a convex cone. Let x ∈ E\(−K) be such that R x + K = E. Then there exists a K-positive linear functional φ: E → R such that φ(x) > 0.

Connection to the Hahn–Banach theorem

Main article: Hahn–Banach theorem

The Hahn–Banach theorem can be deduced from the M. Riesz extension theorem.

Let V be a linear space, and let N be a sublinear function on V. Let φ be a functional on a subspace U ⊂ V that is dominated by N:

$\phi(x) \leq N(x), \quad x \in U.$

The Hahn–Banach theorem asserts that φ can be extended to a linear functional on V that is dominated by N.

To derive this from the M. Riesz extension theorem, define a convex cone K ⊂ R×V by

$K = \left\{ (a, x) \, \mid \, N(x) \leq a \right\}.$

Define a functional φ₁ on R×U by

$\phi_1(a, x) = a - \phi(x).$

One can see that φ₁ is K-positive, and that K + (R × U) = V. Therefore φ₁ can be extended to a K-positive functional ψ₁ on R×V. Then

$\psi(x) = - \psi_1(0, x)$

is the desired extension of φ. Indeed, if ψ(x) > N(x), we have: (N(x), x) ∈ K, whereas

$\psi_1(N(x), x) = N(x) - \psi(x) < 0,$

leading to a contradiction.

References

Riesz, M. (1923), "Sur le problème des moments. III." (in French), Ark. F. Mat. Astr. O. Fys. 17 (16), JFM 49.0195.01
Akhiezer, N.I. (1965), The classical moment problem and some related questions in analysis, New York: Hafner Publishing Co., MR 0184042